Contribution of enthalpy and entropy in molecular association

Background.

In order to accurately describe the interaction between proteins and their partners (cofactors, activators, inhibitors), three actors should be taken into account: the ligand, the protein and the solvent in which both are solvated. From the perspective of the ligand, the complexation with the protein should offer favourable interactions such as hydrogen bonds, charge-charge or π-π interactions, etc. These interactions will add favourably to the enthalpy of binding. On the other hand, upon binding the ligand loses conformational, translational and rotational freedom, resulting in an unfavourable entropic contribution to the binding process. Previously we were able to quantify these contributions for Netropsin binding to the DNA minor groove (Dolenc et al., 2005; Dolenc et al., 2006).

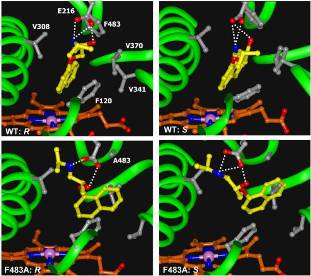
Within the conformational selection model (Carlson, 2002), a protein is considered to be present in an ensemble of different conformations. Low-energy conformations are more likely and will be observed more often, while higher-energy conformations will occur only rarely. A ligand that binds to the active site may only be able to do so if the protein is in a specific conformation. For tightly binding ligands, the favourable ligand-protein enthalpy may then be sufficient to stabilize the protein when it is in a high-energy conformational state. From the perspective of the protein, this is an unfavourable enthalpic contribution. As the ligand now locks the protein in this conformational state, its flexibility is also reduced, leading to an additional unfavourable entropic contribution. This model plays an important role to explain induced fit effects and the modulation of constitutively active receptors. We were able to observe the effect of conformational selection for the metabolic enzyme cytochrome P450 2D6 and the conformational states of its active-site residue Phe483 (Hritz et al., 2008). A well-known contribution to the free energy of binding which is nonetheless often ignored in modelling approaches is formed by the desolvation of the protein and ligand. On the one hand, the loss of direct solvent-ligand and solvent-protein interactions (hydrogen bonds) leads to an unfavourable enthalpic contribution, but on the other hand, these structured water molecules are released to bulk solvent, leading to a favourable increase in entropy. For drug design purposes, special care should additionally be taken if solvent molecules play a role in the binding of the ligand. Efforts to take such water molecules into account accurately and robustly are described with varying amounts of success (Nissink et al., 2002; De Graaf et al., 2006; Vasanthanathan et al., 2009).

Aims and methods.

Ideally, a computational approach to describe ligand binding takes all of the above mentioned contributions into account when estimating the binding affinity. In addition, there is the need to dissect the binding free energy in the enthalpic and entropic contributions in order to better understand the binding process and to modify design strategies accordingly. The aim of this project is to develop the methods and tools to calculate free energies, enthalpies and entropies accurately and efficiently enough to be used in screening programmes.
For free energy calculations, clever thermodynamic cycles (Tembe & McCammon, 1984) may be devised that focus the calculations on differences in which the sampling is most similar. In the free energy calculation, the sampling then needs to be complete for those parts that differ between the two end-states. To accurately calculate enthalpic and entropic differences, the statistical mechanical formulae are readily available (Peter et al., 2004), but these properties depend on ensemble averages of the complete system (protein, ligand and solvent) that need to be converged to a high precision (Reinhard et al., 2001). In the case of enthalpic differences, one needs to subtract two ensemble averages of solvated protein-ligand complexes in order to determine the difference between two ligands. As the total enthalpy of the system is easily four to five orders of magnitude larger than the difference that needs to be determined, this places extreme requirements on the precision and the convergence of the calculations.

Entropy differences for a certain process can be calculated from integration over the correlation of the complete enthalpy of the system and the derivative of this enthalpy with respect to a coupling parameter along the process. As the complete enthalpy again involves all interaction terms, this correlation is extremely difficult to converge (Peter et al., 2004). Alternatively, one can obtain the entropy using Van 't Hoff plots of the free energy change at different temperatures. As several accurate free energy calculations are required, this is still a cumbersome process, but has been applied successfully in various applications (Peter et al., 2004; Carlsson and Aqvist, 2006; Zhou et al., 2006).

For solvation, it was shown already by Ben-Naim that the change in solvent-solvent enthalpy exactly cancels with an entropic term in the free energy (Ben-Naim, 1992). This means that in order to understand the driving forces of solvation, it is not so relevant to look at the experimentally accessible enthalpy and entropy (including the solvent-solvent contribution), but rather one should calculate the so-called solute-solvent enthalpies and entropies (van der Vegt et al., 2004). It turns out that the solvent-solvent interactions are the main reason for the difficulty in convergence for the complete enthalpies and entropies and that the solute-solvent enthalpies and entropies are readily calculated from MD simulations. This also offers an explanation for the fact that the enthalpies and entropies are so much harder to converge, while the free energy converges more easily; the contributions that give most noise exactly cancel in the free energy.

Following the same arguments for the enthalpy-entropy compensation in solvation, we have derived the formulae for ligand binding. When comparing the binding characteristics of two ligands, the relative Helmholtz free energy difference, ΔΔA_bind, can be written as the sum of the ligand-surrounding energy (ΔΔU_D) and the corresponding entropy (ΔΔS_D),

(1) ΔΔA_bind = ΔΔU_D - TΔΔS_D

These terms can be defined such that no terms that refer to the protein-protein, protein-solvent or solvent-solvent interaction energies occur. The effects in these terms upon ligand binding are not zero, but cancel exactly in the enthalpy and entropy. Therefore they do not contribute to the free energy of binding. It can be expected that (as with solvation) these terms are the main cause for convergence problems when calculating the complete enthalpy and entropy, which are experimentally accessible. However, to understand the ligand binding process in terms of the thermodynamics and to adjust drug design strategies accordingly, the well-converging ΔΔU_D and ΔΔS_D of equation (1) are more relevant.

Accurate calculations of enthalpy and entropy differences based on rigorous statistical mechanics for drug design are currently rather uncommon. This project will focus on such calculations, and will investigate the calculation of the ligand-surrounding enthalpies and entropies, as outlined above. The convergence characteristics of full entropy calculations versus ligand-surrounding entropies will be investigated. It is expected that the well-converging ligand-surrounding enthalpies and entropies will be better suitable to explain experimental findings in ligand binding. In the first year, different methods to calculate energies and entropies will be applied and compared. In the second year, special emphasis will be on the determination of the reduced properties. Special care will be taken to validate the methods against model systems and experimental data, in close collaboration with JUNGBAUER. Finally, the role of enhanced sampling techniques for these calculations will be explored in the second half of the project. The overall aim of this project is to develop methods that offer physically meaningful estimates of binding enthalpy and entropy without additional computational costs, as compared to free energy calculations. This highly valuable insight into these features of protein-ligand interactions can be practically attainable in relevant applications.

Ben-Naim, A. (1992) Statistical thermodynamics for chemists and biochemists. New York: Plenum press
Carlson, H. A. (2002) Curr. Opin. Chem. Biol. 6, 447 - 452
Carlsson, J., Åqvist, J. (2006) Phys. Chem. Chem. Phys. 8, 5385 - 5395
De Graaf, C., Oostenbrink, C., Keizers, P. H. J., Van der Wijst, T., Jongejan, A., Vermeulen, N. P. E. (2006) J. Med. Chem. 49, 2417 - 2430
Dolenc, J., Oostenbrink, C., Koller, J., van Gunsteren, W. F. (2005) Nucl. Acids Res. 33, 725 - 733
Dolenc, J., Baron, R., Oostenbrink, C., Koller, J., van Gunsteren, W. F. (2006) Biophys. J. 91, 1460 - 1470
Hritz, J., de Ruiter, A., Oostenbrink, C. (2008) J. Med. Chem. 51, 7469 - 7477
Nissink, J. W. M., Murray, C. W., Hartshorn, M. J., Verdonk, M. L., Cole, J. C., Taylor, J. B. (2002) Proteins 49, 457 - 471
Peter, C., Oostenbrink, C., van Dorp, A., van Gunsteren, W. F. (2004) J. Chem. Phys. 120, 2652 - 2661
Reinhardt, W. P., Miller, M. A., Amon, L. M. (2001) Acc. Chem. Res. 34, 607 - 614
Tembe, B. L., McCammon, J. A. (1984) Comput. Chem. 8, 281 - 283
van der Vegt, N. F. A., van Gunsteren, W. F. (2004) J. Phys. Chem. B 108, 1056 - 1064
Vasanthanathan, P., Hritz, J., Taboureau, O., Olsen, L., Jorgensen, F. S., Vermeulen, N. P. E., Oostenbrink, C. (2009) J. Chem. Inf. Model. 49, 43 - 52
Zhou, Y., Oostenbrink, C., Jongejan, A., van Gunsteren, W. F., Hagen, W. R., de Leeuw, S. W., Jongejan, J. A. (2006) J. Comput. Chem. 27, 857 - 867